حل معادلات، در متلب (MATLAB) (در نسخه های قدیمی)
در متلب، می توان با دو دستور solve یا fzero ، معادلات شامل متغیرها را حل نمود.
دستور
solve در نسخه های قدیمی متلب (MATLAB)، تعریف معادلات را به صورت ذکر شده در بین علامت های
' دریافت می کرد (مثل کد
solve('x+2*y=7','x-y=1') )، اما در نسخه های جدید متلب (MATLAB)، دیگر علامت
' در تعریف معادله به کار نمی رود و به جای آن، از دستور
syms برای تعریف متغیرها به صورت سمبلیک (Symbolic) و همچنین ازعلامت های
== در تعریف معادله استفاده می شود (مثل کدهای
syms x y و
solve(x+2*y==7, x-y==1) ).
با توجه به این نکته، این آموزش برای نسخه های قدیمی متلب (MATLAB) است.
دستور solve :
دستور solve در متلب، برای حل معادلات چندجمله ای به کار می رود.
نتیجه :
دقت شود که معادله باید بین علامت ' قرار بگیرد.
دو پاسخ معادله در خروجی نمایش داده شده است. دو پاسخ معادله، پاسخ های دقیق معادله می باشند و چنانچه بخواهیم آنها را به صورت عددی ببینیم باید دستور double(ans) و یا vpa(ans) را اجرا کنیم. به عنوان مثال با دستور double داریم :
نتیجه :
و با دستور vpa داریم :
نتیجه :
دستور solve همچنین قادر است که معادلات شامل دو متغیر را حل نماید :
نتیجه :
دقت شود چون می خواهیم متغیر y را بر حسب x به دست آوریم، باید عبارت 'y' را پس از معادله بنویسیم .
چنانچه دو معادله بر حسب x و y داشته باشیم، آنگاه می توان مقادیر دو متغیر x و y را به دست آورد :
نتیجه :
این دو معادله دارای دو سری پاسخ است، پاسخ سری اول x(1) و y(1) و پاسخ سری دوم x(2) و y(2) می باشد. چنانچه پاسخ اول مورد نظر ما باشد، می نویسیم :
نتیجه :
دقت شود که در کد قبل، پاسخ دو معادله را به بردار [x,y] نسبت دادیم و پاسخ ها در خروجی نمایش داده شدند. چنانچه پاسخ دو معادله را به بردار [x,y] نسبت ندهیم، آنگاه پاسخ ها در خروجی نمایش داده نمی شوند :
نتیجه :
برای دیدن مقادیر بردارهای x و y ، کافی است که دستورات solution.x و solution.y را اجرا کنید :
نتیجه :
پاسخ سری اول solution.x(1) و solution.y(1) و پاسخ سری دوم solution.x(2) و solution.y(2) می باشد. چنانچه پاسخ اول مورد نظر ما باشد می نویسیم :
نتیجه :
برخی معادلات نمی توانند به صورت سمبلیک حل شوند و در اینگونه موارد دستور solve سعی می کند که یک حل عددی را بیابد. به مثال زیر توجه کنید :
نتیجه :
در بعضی موارد، معادله بیش از یک پاسخ دارد و دستور solve پاسخی را برمی گرداند که مد نظر ما نبوده است. به عنوان مثال :
معادله زیر را در نظر بگیرید :
\[ {e^{ - x}} = \sin (x) \]معادله را با استفاده از دستور solve حل می کنیم :
نتیجه :
به شکل زیر توجه کنید :
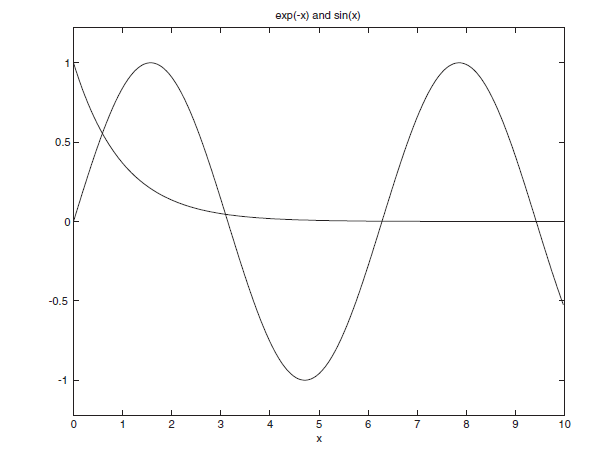
با توجه به شکل بالا، پاسخ دیگری مد نظر ما بوده است که حدود $ x = 3 $ می باشد. چنانچه بخواهیم این پاسخ را به دست آوریم باید از دستور fzero در متلب استفاده کنیم که در ادامه در مورد آن توضیح خواهیم داد.
دستور fzero :
همان مثال قبل را این بار با fzero حل می کنیم و برای دستور fzero مشخص می کنیم که پاسخ نزدیک $ x = 3 $ را بیابد :
نتیجه :
بنابراین دستور fzero دقیقا همان پاسخ مد نظر ما که نزدیک $ x = 3 $ می باشد را برگرداند.
دقت شود که در تعریف معادله، از علامت = استفاده نکردیم و دستور به طور خودکار، عبارت درون دو علامت ' را برابر صفر قرار می دهد.
 فرهاد
فرهاد سلام و خسته نباشین .0=(0.4164sin(6t)+.017sin(14.49t
ببخشید من این معادله رو به این روشهایی که گفتین نمیتونم حل کنم
 رضا
رضا سلام میخاستم معادله x*tan(x)=3.896*10^-6 را چطور میشه حل کرد
مقادیر مختلف x را میخاستم
و میخاستم بدونم میشه رسمش کرد
با تشکر
 aryan
aryan سلام من با این کد ها مشکل دارم حل نمیشه
s=solve('(108354-Z0)*(-4.617*(cosd(p)*cosd(k))+0.392*(-cosd(p)*cosd(k))-151.992*(sind(p)))/(-4.617*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+0.392*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=4296851-X0','(108354-Z0)*(-4.617*(sind(w)*sind(p)*cosd(k)+cosd(w)*sind(k))+0.392*(-sind(w)*sind(p)*sind(k)+cosd(w)*cosd(k))-151.992*(-sind(w)*cosd(p)))/(-4.617*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+0.392*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=4233813-Y0','(123791-Z0)*(87.296*(cosd(p)*cosd(k))+(-0.309)*(-cosd(p)*cosd(k))-151.992*(sind(p)))/(87.296*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+(-0.309)*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=4553579-X0','(123791-Z0)*(87.296*(sind(w)*sind(p)*cosd(k)+cosd(w)*sind(k))+(-0.309)*(-sind(w)*sind(p)*sind(k)+cosd(w)*cosd(k))-151.992*(-sind(w)*cosd(p)))/(87.296*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+(-0.309)*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=4473130-Y0','(112791-Z0)*(83.690*(cosd(p)*cosd(k))+(-100.003)*(-cosd(p)*cosd(k))-151.992*(sind(p)))/(83.690*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+(-100.003)*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=5483104-X0','(112791-Z0)*(83.690*(sind(w)*sind(p)*cosd(k)+cosd(w)*sind(k))+(-100.003)*(-sind(w)*sind(p)*sind(k)+cosd(w)*cosd(k))-151.992*(-sind(w)*cosd(p)))/(83.690*(-cosd(w)*sind(p)*cosd(k)+sind(w)*sind(k))+(-100.003)*(cosd(w)*sind(p)*sind(k)+sind(w)*cosd(k))-151.992*(cosd(w)*cosd(p)))=3900089-Y0')
s=[s.X0 x.Z0 s.p s.k s.w s.Y0]
تصویر ارور رو زمینه میکنم...
 تینا
تینا سلام برای استفاده از genfis3 در متلب باید چ کدی بنویسم ؟من برای مدل انفیس ۷ورودی دارم ک درgenfis1 اخطار نبود حافظه میده .لطفا کمکم کنین...
 مهدی
مهدی سلام
من در حل معادله حالت موندم
یه سوال سه قسمته هست
تو قسمت اول حل از طریق معادله ردیچ وانگ
تو قسمت دوم حل از طریق ردیچ وانگ سو
 سپهر
سپهر سلام
من عین همین کد که اینجا هست رو توی کامند متلب کپی میکنم ولی برنامه هنگ میکنه!
A=solve('x^2-2*x-4=0');
B=double(A)
 mas
mas your version mathlab is low.install update version
 احسان
احسان منم همین مشکلو دارم ورژن متلبمم R2018b هست
 RRR
RRR سلام
من برا اینکه بتونم چندتا سوال درس استاتیک رو تو متلب پیاده کنم باید کدوم بخش نرم افزار رو یاد بگیرم؟
 محمد
محمد سلام ببخشید برای حل معادله ۲۴ معادله ۲۴ مجهول در متلب چقدر زمان میخواد؟برنامه ی من سه روزه در حال رانه اما جواب نداده.لطفا راهنمایی کنید
 محمد
محمد تو رو خدا اگه کسی میدونه جواب بده خیلی ضروریه
چقد زمان برای حل معادله ۲۴ معادله ۲۴ مجهول میخواد.من ماتریسی نوشتم
 mohammad ahwazi
mohammad ahwazi بسیار مفید و کامل و مختصر بدون توضیحات اضافه احسنت بر شما
 یکی
یکی خیلی مفید مختصر عاااااااالی بود