یافتن یک پاسخ خاص از بین پاسخ های معادله (پاسخ خاص موجود در یک بازه خاص یا در نزدیکی یک نقطه خاص)، با دستور fzero ، در متلب (MATLAB)
هنگامی که یک معادله داریم و می خواهیم پاسخ آن را به دست آوریم، اگر آن معادله بیش از یک پاسخ داشته باشد و ما یک پاسخ خاص مد نظرمان باشد، می توانیم دستور fzero در متلب (MATLAB) را به کار ببریم تا همان پاسخ خاص را به ما بدهد.
برای دستور fzero مشخص می کنیم که پاسخ مورد نظر ما در نزدیکی کدام نقطه است و یا اینکه در چه بازه ای قرار گرفته است، آنگاه دستور fzero همان پاسخ خاص را برمی گرداند.
در متلب (MATLAB)، دستور solve نیز برای حل معادلات به کار می رود، ولی دستور solve ممکن است پاسخی غیر از آنچه مد نظر ما بوده است را برگرداند، ولی fzero این مشکل را ندارد. برای اینکه تفاوت دو دستور solve و fzero را به خوبی متوجه شوید، مثالی می زنیم که بتوانیم نتیجه آن دو را مقایسه کنیم :
معادله زیر را در نظر بگیرید :
\[ {e^{ - x}} = \sin (x) \]
ابتدا معادله را با استفاده از دستور solve حل می کنیم :
3 خط اول کدها، برای عدم تداخل برنامه فعلی با برنامه های قبلی اجرا شده در متلب (MATLAB) می باشد.
نتیجه :
به شکل زیر توجه کنید :
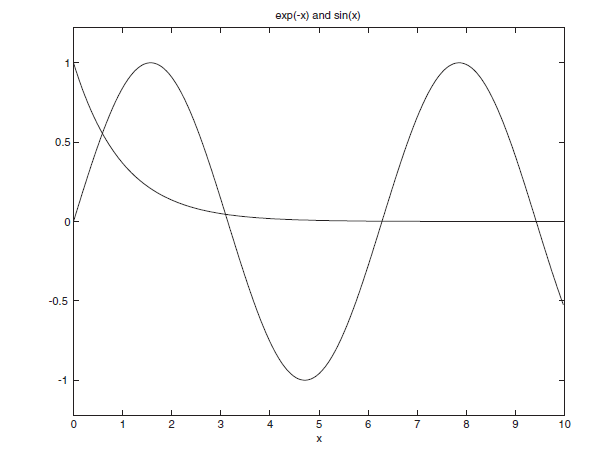
با توجه به شکل بالا، پاسخ دیگری مد نظر ما بوده است که حدود
$ x = 3
$ می باشد. چنانچه بخواهیم این پاسخ را به دست آوریم باید از دستور fzero استفاده کنیم. بنابراین کد متلب (MATLAB) زیر را می نویسیم :
عدد 3 که در پرانتز دستور fzero نوشته ایم، تعیین می کند که دستور fzero پاسخی را بیابد که در نزدیکی
$ x = 3
$ قرار دارد.
نتیجه :
بنابراین دستور fzero دقیقا همان پاسخ مد نظر ما که نزدیک
$ x = 3
$ می باشد را برگرداند.
دقت شود که در تعریف معادله، از علامت = استفاده نکردیم و دستور به طور خودکار، عبارت درون دو علامت ' را برابر صفر قرار می دهد.
معادله زیر را در نظر بگیرید :
\[ \sin (x) = 0 \]می خواهیم پاسخ آن در نزدیکی $ x = 3 $ را به دست آوریم :
نتیجه :
یافتن ریشه (Root) (پاسخ) در یک بازه خاص :
به مثال زیر توجه کنید :
معادله زیر را در نظر بگیرید :
\[ \cos (x) = 0 \]می خواهیم پاسخ آن در بازه $ \left[ {\matrix{ 1 & 2 \cr } } \right] $ را به دست آوریم :