رسم یک تابع در مختصات قطبی (Polar Coordinate)، با دستور ezpolar ، در متلب (MATLAB)
در مختصات قطبی (Polar Coordinate)، اطلاعات نقاط بر اساس دو مقدار فاصله از مرکز محورهای مختصات (r) و زاویه نسبت به محور x (محور افقی) (زاویه تتا - Theta) می باشند.
چنانچه تابعی داشته باشیم که در آن، r بر حسب تتا ( $ \theta $ ) بیان شده باشد ( f تابعی بر حسب $ \theta $ می باشد) :
\[ r = f(\theta ) \]آنگاه می توانیم تابع مورد نظر (تابع f) را با دستور ezpolar در متلب (MATLAB)، رسم کنیم.
رسم برای بازه زیر از $ \theta $ صورت می گیرد :
\[ 0 < \theta < 2\pi \]یا اگر بخواهیم که رسم برای یک بازه خاص از $ \theta $ صورت گیرد، باید آن بازه را در پرانتز دستور ezpolar ذکر نماییم.
در این نوع رسم، یک دایره رسم می گردد که بر روی محیط آن، اعداد 0 تا 360 درجه نوشته می شود (چون $ \theta $ بر حسب زاویه می باشد) و سپس برای هر مقدار $ \theta $ ، مقدار r متناظر با آن، به صورت یک نقطه با فاصله ای از مرکز دایره که برابر مقدار r می باشد، رسم می کنیم. بنابراین شکل نهایی، یک منحنی حاصل از اتصال نقاط مورد نظر خواهد بود.
به مثال زیر توجه کنید :
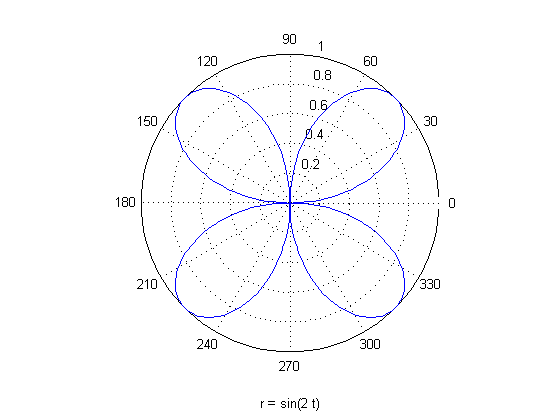
قصد داریم که تابع زیر را برای بازه $ 0 < \theta < 2\pi $ رسم کنیم ( f تابعی بر حسب $ \theta $ می باشد) :
\[ r = f(\theta ) = \sin (2\theta ) \]بنابراین کد متلب (MATLAB) زیر را می نویسیم :
close all
clc
ezpolar('sin(2*t)')
3 خط اول کدها برای عدم تداخل برنامه فعلی با برنامه های قبلی اجرا شده در متلب (MATLAB) می باشد.
نتیجه :
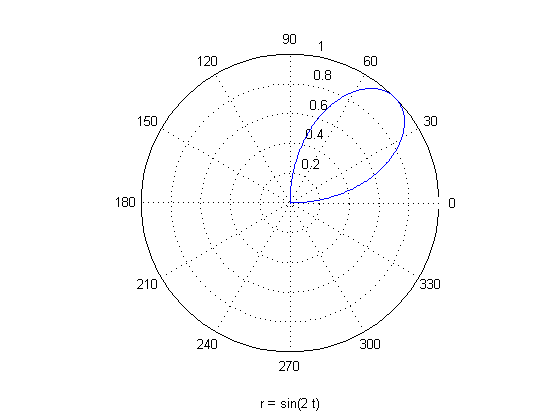
مثال قبل را این بار برای بازه زیر از $ \theta $ رسم می کنیم :
\[ 0 < \theta < \frac{\pi }{2} \]close all
clc
ezpolar('sin(2*t)',[0,pi/2])
همان طور که مشاهده می کنید، بازه $ \theta $ در پرانتز دستور ezpolar ذکر شده است.
نتیجه :
مثال help نرم افزار متلب (MATLAB) :
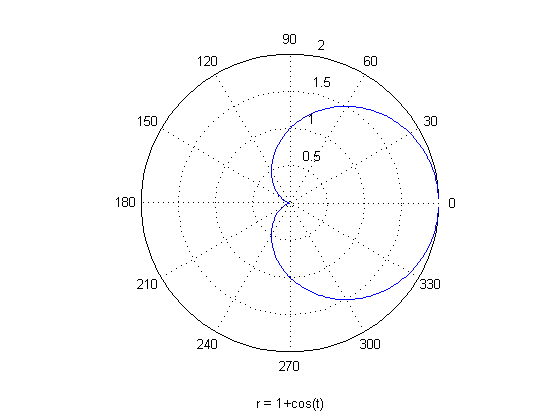
قصد داریم که تابع زیر را برای بازه $ 0 < \theta < 2\pi $ رسم کنیم ( f تابعی بر حسب $ \theta $ می باشد) :
\[ r = f(\theta ) = 1 + \cos (\theta ) \]بنابراین کد متلب (MATLAB) زیر را می نویسیم :
close all
clc
ezpolar('1+cos(t)')
نتیجه :