ساخت آرایه ها برای توابع چند بعدی، با دستور ndgrid ، در متلب (MATLAB)
با استفاده از دستور ndgrid در متلب (MATLAB)، می توانیم آرایه هایی را برای توابع چند بعدی بسازیم. توضیحات کامل تر را با یک مثال شرح می دهیم :
فرض کنید می خواهیم تابع دو بعدی z را به صورت یک ماتریس دو بعدی، بر حسب مقادیر مختلف x و y ، به صورت زیر بسازیم و سپس آن را رسم کنیم :
\[ \begin{align} z=\sqrt{x^2+y^2} \end{align} \]بازه تعریف شده برای x را به صورت (-5,5) و بازه تعریف شده برای y را به صورت (-4,4) در نظر می گیریم. همچنین، فاصله نمونه های گسسته از این بازه ها را برابر 0.1 قرار می دهیم. برای آنکه سودمندی استفاده از دستور ndgrid را نشان بدهیم، ابتدا روش های دیگر را برای ساخت z به کار می بریم و سپس از دستور ndgrid استفاده می کنیم تا متوجه شوید که استفاده از دستور ndgrid ، ساده ترین راه است. ابتدا با روش سخت تر، این کار را انجام می دهیم :
دستور length ، برای تعیین طول یک بردار است و دستور zeros ، برای ساخت یک ماتریس با عناصر برابر صفر، به کار می رود. دستور mesh نیز برای رسم یک ماتریس دو بعدی، به صورت سیمی (mesh)، به کار می رود. دستورات xlabel و ylabel و zlabel ، برای تعیین عنوان برای محورهای مختصات می باشند.
نتیجه :
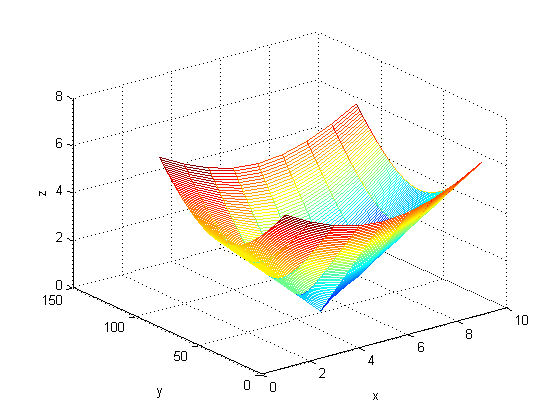
این بار ساخت z را با دستور ndgrid انجام می دهیم :
دقت شود که علامت نقطه (.) برای آن است که هر عنصر از x و y ، به توان 2 برسد، نه اینکه کل بردار x یا بردار y ، به توان 2 برسد.
نتیجه :

مشاهده می کنید که استفاده از دستور ndgrid ، حجم کدها را بسیار کم می کند و مناسبترین روش می باشد.
اگر ماتریس مورد نظرمان، بیش از 2 بعد داشته باشد، که دیگر استفاده از دستور ndgrid واجب است و روش های دیگر واقعا سخت می باشند.
شاید به نظرتان برسد که بدون دستور ndgrid و همچنین بدون حلقه های for و تنها با استفاده از علامت نقطه (.) می توانیم ساخت z را به صورت زیر انجام دهیم، اما این کار ایجاد خطا می کند :
نتیجه :
مشاهده می کنید که یک پیام خطا نمایش داده شده است.