هاشور زدن (رنگی کردن) بخشی از منحنی های رسم شده (بالای منحنی ها، پایین منحنی ها، بین منحنی ها و ...) ، با دستور fill ، در متلب (MATLAB)
با استفاده از دستور fill در متلب، می توانیم بخش های دلخواهی از منحنی های رسم شده را هاشور بزنیم (رنگی کنیم). دستور fill ، در واقع برای کشیدن یک چندضلعی که داخل آن با رنگ خاصی پر شده است، به کار می رود، اما ما از این قابلیت آن استفاده کرده و عمل هاشور زدن (رنگی کردن) بخش های دلخواه از شکل و منحنی ها را انجام خواهیم داد. ابتدا نحوه کشیدن چندضلعی با دستور fill را شرح می دهیم و سپس مثال های پیچیده تری را شرح می دهیم که در آنها بخش هایی از منحنی های رسم شده را به صورت هاشورزده (رنگی) در خواهیم آورد.
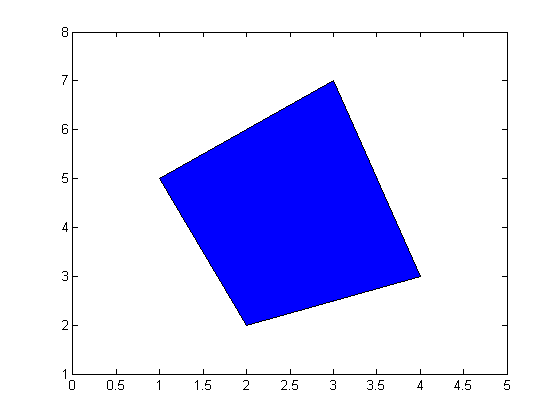
رسم یک چندضلعی با رنگ دلخواه با استفاده از دستور fill در متلب :
برای رسم یک چندضلعی با دستور fill در متلب، باید مختصات نقاط آن چند ضلعی را بدانیم و سپس مختصات آنها را در دو بردار X و Y بنویسیم که بردار X شامل مختصات x نقاط چندضلعی و بردار Y شامل مختصات y نقاط چند ضلعی می باشد. سپس دستور fill ، با دریافت دو بردار X و Y ، چندضلعی را رسم خواهد کرد.
به مثال زیر توجه کنید :
close all
clc
X=[1 2 4 3];
Y=[5 2 3 7];
fill(X,Y,'b');
axis([0 5 1 8])
سه خط اول، دستورات متداول برای عدم تداخل با برنامه های پیشین اجرا شده در متلب می باشند.
دقت شود که با عبارت 'b' در پرانتز دستور fill ، مشخص کرده ایم که داخل چند ضلعی، با رنگ آبی پر شود. با دستور axis نیز حدود محورهای مختصات را مشخص کرده ایم.
نتیجه :
هاشور زدن (رنگی کردن) بخشی از یک منحنی رسم شده با دستور fill در متلب :
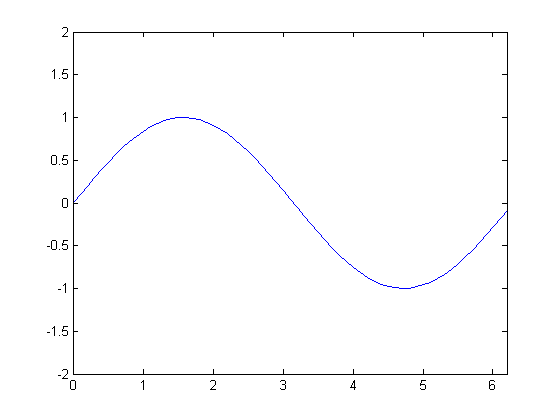
گاهی پیش می آید که توسط نرم افزار متلب، یک منحنی را رسم می کنیم و پس از مشاهده آن نیاز داریم که بخشی از آن را به صورت هاشورزده (رنگی) درآوریم. به عنوان مثال فرض کنید با کدهای زیر یک منحنی را رسم کنیم :
close all
clc
x=0:0.1:2*pi;
y=sin(x);
plot(x,y)
axis([0 x(end) -2 2])
منظور از x(end) ، آخرین عنصر بردار x می باشد.
نتیجه :
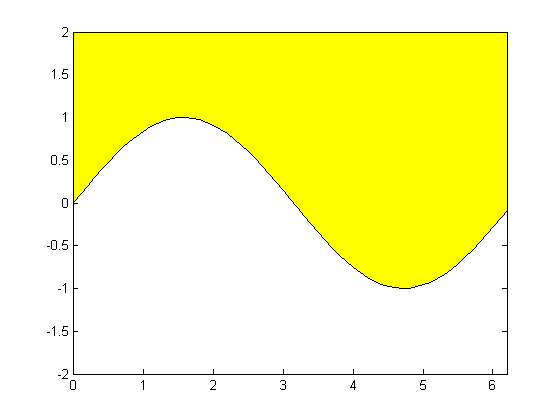
حال فرض کنید که بخواهیم بالای این منحنی را با رنگ زرد هاشور بزنیم. برای این منظور، اینگونه از دستور fill استفاده خواهیم کرد :
close all
clc
x=0:0.1:2*pi;
y=sin(x);
plot(x,y)
X=[0,x,2*pi];
Y=[2,y,2];
fill(X,Y,'y');
axis([0 x(end) -2 2])
دقت شود که در تعریف دو بردار X و Y که به دستور fill داده می شوند، از همان دو بردار x و y استفاده کرده ایم، اما علاوه بر این، به این دو بردار، دو نقطه نیز اضافه کرده ایم. این دو نقطه را با توجه به همان شکل قبل مشخص کرده ایم، یک نقطه، همان نقطه گوشه بالا سمت چپ شکل با مختصات [x,y]=[0,2] می باشد که باید مختصات آن حتما در ابتدای بردارهای X و Y قرار داده شود و نقطه دوم، همان نقطه گوشه بالا سمت راست شکل با مختصات [x,y]=[2*pi,2] می باشد که باید مختصات آن، حتما در انتهای بردارهای X و Y قرار داده شود. خوب بنابراین با نقاط تعریف شده در بردارهای X و Y ، همان فضای بسته ای که می خواستیم رنگی شود را انتخاب کرده ایم.
نتیجه :
هاشور زدن (رنگی کردن) بخش های مشترک یا غیر مشترک (هر بخش دلخواه) حاصل از رسم دو منحنی :
در برخی موارد نیاز است که بخش های مشترک یا غیر مشترک حاصل از رسم دو منحنی را هاشور بزنیم (رنگی کنیم). پیچیدگی این مورد، خیلی بیشتر از حالت یک منحنی نیست و تنها باید حواسمان باشد که بخشی را که می خواهیم هاشور بزنیم به طور درست با دو بردار X و Y تعریف کنیم. به مثال زیر توجه کنید :
ابتدا دو منحنی را به صورت عادی رسم می کنیم :
close all
clc
hold on
x=0:0.1:2*pi;
y_1=sin(x);
plot(x,y_1,'+r')
y_2=0.5*x-1;
plot(x,y_2,'^g')
axis([0 x(end) -2 3])
نتیجه :
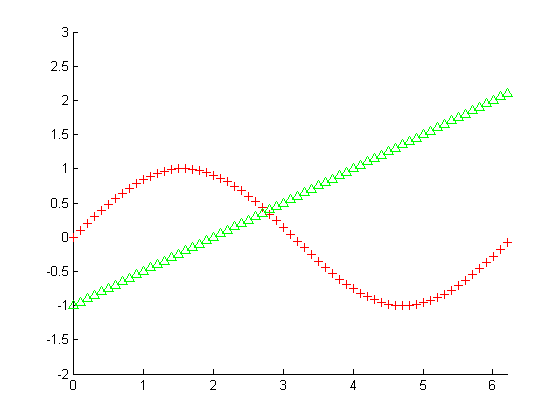
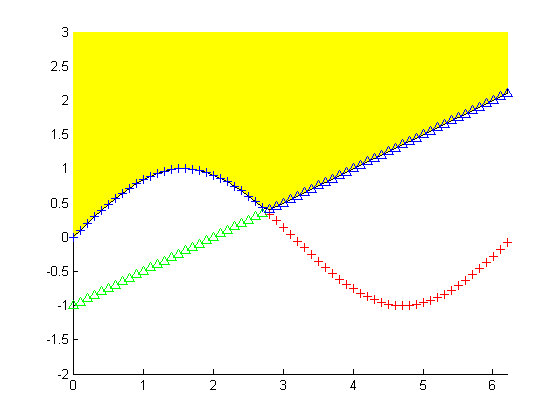
اکنون قصد داریم بین هر دو منحنی، برای هر x ، مقدار ماکزیمم y را مشخص کرده و نقاط ماکزیمم را با رنگ آبی نمایش دهیم و همچنین بالای این مقادیر ماکزیمم (بالای نمودار) را با رنگ زرد پر کنیم. برای این منظور کدهای زیر را می نویسیم :
close all
clc
hold on
x=0:0.1:2*pi;
y_1=sin(x);
plot(x,y_1,'+r')
y_2=0.5*x-1;
plot(x,y_2,'^g')
axis([0 x(end) -2 3])
L=length(x);
maximum=zeros(1,L);
for nn=1:L
maximum(nn)=max(y_1(nn),y_2(nn));
end
X=[0,x,2*pi];
Y=[3,maximum,3];
fill(X,Y,'y')
plot(x(1:28),y_1(1:28),'+b');
plot(x(29:end),y_2(29:end),'^b');
ابتدا دو نمودار را به صورت معمولی رسم کرده ایم. دستور length ، تعداد عناصر بردار را مشخص می کند. سپس برداری به نام maximum تعریف کردیم که در آن برای هر x ، مقدار ماکزیمم y از بین دو مقدار مربوط به دو منحنی، مشخص شده است. دستور
max ، مقدار ماکزیمم را تعیین می کند. سپس با دستور fill ، بخش بالای مقادیر ماکزیمم (بالای نمودار) را با رنگ زرد پر کرده ایم. در دو خط آخر نیز، با دو دستور plot ، نقاط ماکزیمم را دوباره، اما این بار با رنگ آبی، رسم کرده ایم. دو عدد 28 و 29 نوشته شده در این دو خط، همان شماره نقاط نزدیک تلاقی دو نمودار است که آنها را از دیدن نمودارهای رسم شده، متوجه شده ایم.
نتیجه :
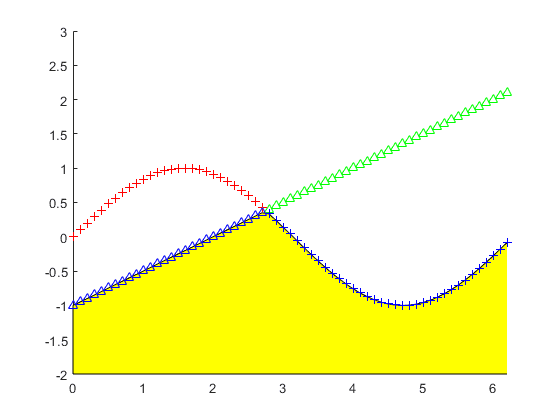
اکنون قصد داریم بین هر دو منحنی، برای هر x ، مقدار مینیمم y را مشخص کرده و نقاط مینیمم را با رنگ آبی نمایش دهیم و همچنین پایین این مقادیر مینیمم (پایین نمودار) را با رنگ زرد پر کنیم. برای این منظور کدهای متلب (MATLAB) زیر را می نویسیم :
close all
clc
hold on
x=0:0.1:2*pi;
y_1=sin(x);
plot(x,y_1,'+r')
y_2=0.5*x-1;
plot(x,y_2,'^g')
axis([0 x(end) -2 3])
L=length(x);
minimum=zeros(1,L);
for nn=1:L
minimum(nn)=min(y_1(nn),y_2(nn));
end
X=[0,x,2*pi];
Y=[-2,minimum,-2];
fill(X,Y,'y')
plot(x(1:28),y_2(1:28),'^b');
plot(x(29:end),y_1(29:end),'+b');
ابتدا دو نمودار را به صورت معمولی رسم کرده ایم. دستور length ، تعداد عناصر بردار را مشخص می کند. سپس برداری به نام minimum تعریف کردیم که در آن برای هر x ، مقدار مینیمم y از بین دو مقدار مربوط به دو منحنی، مشخص شده است. دستور
min ، مقدار مینیمم را تعیین می کند. سپس با دستور fill ، بخش پایین مقادیر مینیمم (پایین نمودار) را با رنگ زرد پر کرده ایم. در دو خط آخر نیز، با دو دستور plot ، نقاط مینیمم را دوباره، اما این بار با رنگ آبی، رسم کرده ایم. دو عدد 28 و 29 نوشته شده در این دو خط، همان شماره نقاط نزدیک تلاقی دو نمودار است که آنها را از دیدن نمودارهای رسم شده، متوجه شده ایم.
نتیجه :
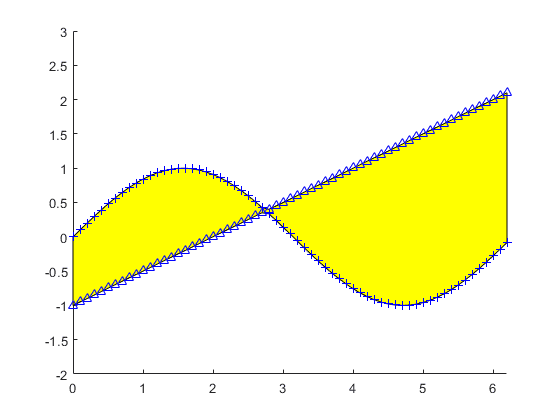
چنانچه بخواهیم که بخش قرار گرفته در بین دو منحنی را با رنگ زرد پر کنیم و همچنین نقاط دور تا دور آن را هم با رنگ آبی نمایش بدهیم، کد متلب (MATLAB) زیر را اجرا می کنیم :
close all
clc
hold on
x=0:0.1:2*pi;
y_1=sin(x);
plot(x,y_1,'+r')
y_2=0.5*x-1;
plot(x,y_2,'^g')
axis([0 x(end) -2 3])
L=length(x);
maximum=zeros(1,L);
minimum=zeros(1,L);
for nn=1:L
maximum(nn)=max(y_1(nn),y_2(nn));
minimum(nn)=min(y_1(nn),y_2(nn));
end
x_flip=flip(x);
maximum_flip=flip(maximum);
X=[x,x_flip];
Y=[minimum,maximum_flip];
fill(X,Y,'y')
plot(x,y_1,'+b');
plot(x,y_2,'^b');
برداری به نام maximum تعریف کردیم که در آن برای هر x ، مقدار ماکزیمم y از بین دو مقدار مربوط به دو منحنی، مشخص شده است. همچنین برداری به نام minimum تعریف کردیم که در آن برای هر x ، مقدار مینیمم y از بین دو مقدار مربوط به دو منحنی، مشخص شده است.
دستور flip برای معکوس کردن ترتیب عنصرهای بردارهای
x و maximum به کار رفته است، زیرا وقتی می خواهیم فضای بسته مورد نظرمان که باید رنگی شود را بر اساس مختصات نقاط دور آن مشخص کنیم، باید ترتیب نقاط رعایت شود و بنابراین نقاط را به این ترتیب در نظر گرفته ایم که ابتدا نقاط مینیمم را از پایین سمت چپ نمودارها تا پایین سمت راست نمودارها ذکر نموده ایم (بردار minimum ) و سپس نقاط ماکزیمم از بالا سمت راست نمودار تا بالا سمت چپ نمودار را ذکر کرده ایم (ترتیب معکوس عنصرهای بردار maximum ).
نتیجه :
فاطمه عااااااااااااااااالیییییییییی بود
خیلی ممنون از زحماتتون 